# Tree Isomorphism

Problem: how to tell if two trees have the same structure.

Idea: find a way to encode the structure into a string, such that isomorphic trees map to the same string, and non-isomorphic trees map to different strings. Then use string comparison which is easy.

# 1 Encoding

# 1.1 Tree

Let V be the set of vertices of the tree, then the algorithm proceeds by labeling leaves (L) and merging them into the body (B) at its boundary (N, for neighbour).

# 1.1.1 Pseudocode

L := { (v, "v") : v <- V, degree(v) = 1 }
B := V - fst(L)
if |B| <= 2
  l = |B| ++ "(" ++ concat(sort(snd(L))) ++ ")"
  return l
loop
  N := { (v, "(" ++ concat(sort(snd(n))) ++ ")")
       : v <- B
       , n := { l : l <- L, (v, fst(l)) in E }
       , |n| = degree(v) - 1
       }
  if |B| <= 2
    l = |B| ++ "(" ++ concat(sort(snd(N))) ++ ")"
    return l
  L := union(L, N)
  B := B - fst(N)

# 1.1.2 Haskell

The precondition that the Tree is actually a tree is not checked.

import Data.List as List
import Data.Map as Map
import Data.Set as Set

type Tree v = (Set v, Map v (Set v))

degree :: Ord v => Tree v -> v -> Int
degree (_, es) v = maybe 0 Set.size (v `Map.lookup` es)

label :: Map k String -> String
label = concat . sort . Map.elems

neighbours :: Ord v => Tree v -> v -> [v]
neighbours (_, es) v = maybe [] Set.toList (v `Map.lookup` es)

encode :: Ord v => Tree v -> String
encode t@(vs, es) =
  let l0 = Map.fromList
             [ (v, "v")
             | v <- Set.toList vs
             , degree t v == 1
             ]
      b0 = vs `Set.difference` Map.keysSet l0
      loop ls bs =
        let ns = Map.fromList
                   [ (v, "(" ++ label n ++ ")")
                   | v <- Set.toList bs
                   , let n = Map.fromList
                               [ (u, ls Map.! u)
                               | u <- neighbours t v
                               , u `Map.member` ls
                               ]
                   , Map.size n == degree t v - 1
                   ]
        in  if Set.size bs <= 2
              then show (Set.size bs) ++ "(" ++ label ns ++ ")"
              else
                let ls' = ls `Map.union` ns
                    bs' = bs `Set.difference` Map.keysSet ns
                in  loop ls' bs'
  in  if Set.size b0 <= 2
        then show (Set.size b0) ++ "(" ++ label l0 ++ ")"
        else loop l0 b0

# 1.1.3 C++

The Haskell implementation above is translated from some messy C++ code using the standard template library.

I can extract it from its surrounding project and clean it up if necessary, just ask if you want it.

# 1.1.4 Examples

tree encoded
(,) “0()”
({0},) “1()”
({0,1},{0:{1},1:{0}}) “0(vv)”
({0,1,2},{0:{1},1:{0,2},2:{1}}) “1(vv)”
({0,1,2,3},{0:{1},1:{0,2},2:{1,3},3:{2}}) “2(vv)”
({0,1,2,3},{0:{1,2,3},1:{0},2:{0},3:{0}}) “1(vvv)”
({0,1,2,3,4,5,6},{0:{1},1:{0,2},2:{1,3,6},3:{2,4},4:{3,5},5:{4},6:{2}}) “2(((v))((v)v))”

The last example with 7 vertices is the smallest that has more than two arms of different lengths, which exercises all of the conditions of the algorithm.

It is highlighted in red in this diagram of all 11 non-isomorphic trees with 7 nodes:

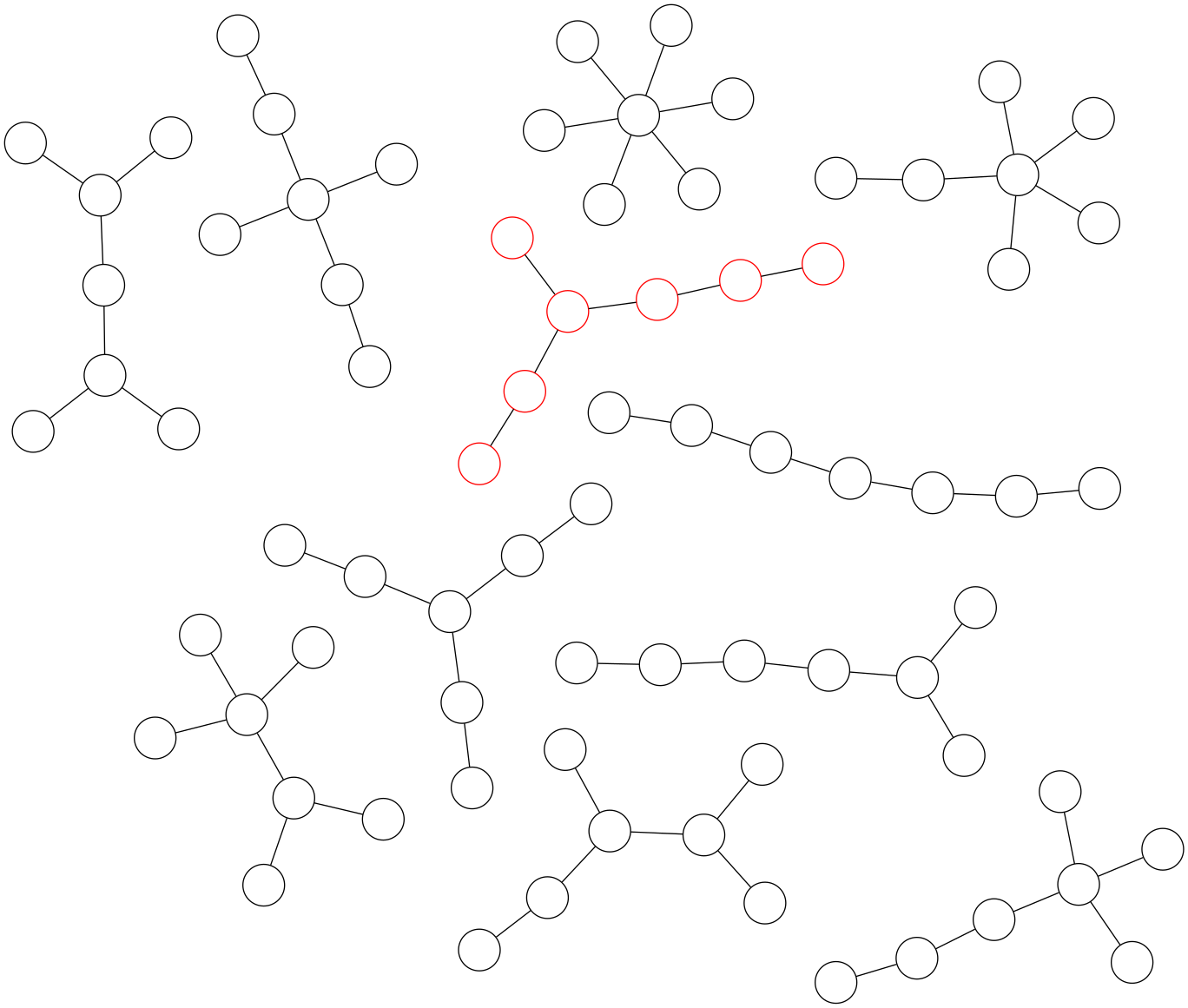
11 trees with 7 nodes

# 1.2 Forest

Encode each tree, sort, concat.

# 1.3 Hyperforest

Convert hypergraph to bipartite graph.

If the hypergraph is a hyperforest, the graph will be a forest.

# 2 Decoding

TODO

# 3 Counting

Number of trees with n unlabeled nodes:

Number of forests with n unlabeled nodes:

Number of forests with n unlabeled nodes and no isolated vertices:

Number of hyperforests with n unlabeled nodes, no isolated vertices, and minimum edge size 2:

# 4 References